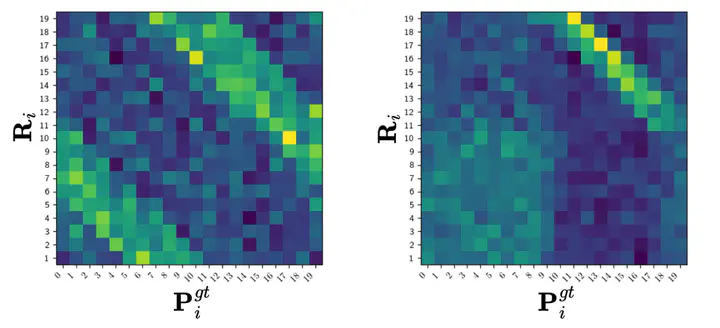
Abstract
Traditional group equivariant methods presuppose known groups, an assumption that can be unrealistic for real-world datasets and potentially too restrictive for neural network architectures. Typically, equivariance in neural networks is implemented through group transformations applied to a canonical weight tensor, facilitating weight sharing across a specified group GG. In this study, we introduce a method to learn such weight-sharing schemes. Our approach involves developing a set of learnable, doubly stochastic matrices that function as soft permutation matrices on canonical weight tensors, accommodating regular group representations as a specific instance. This allows for adaptive kernel transformations that are optimized in conjunction with downstream tasks. Our results demonstrate that when datasets display pronounced symmetries, the learned permutation matrices approximate regular group representations, effectively transforming our weight-sharing networks into standard group convolutional networks.